Ejemplos de longitud de arco
Tiempo después de haber ofrecido información relacionada a las diversas acepciones y aplicaciones del término longitud, en EjemplosDe.com.mx volvemos a hacer foco en esta noción pero, en esta oportunidad, desde una perspectiva más profunda y concreta para poder explicar en qué consiste la idea de longitud de arco.
 Según se advierte al buscar datos relacionados a esta expresión, fueron los matemáticos los impulsores de este concepto que adquiere una gran relevancia frente al proceso de rectificar una curva. Se trata de un cálculo clave para determinar, por medio de fórmulas específicas, cuál ha sido la distancia cubierta por la extensión de una curva.
Según se advierte al buscar datos relacionados a esta expresión, fueron los matemáticos los impulsores de este concepto que adquiere una gran relevancia frente al proceso de rectificar una curva. Se trata de un cálculo clave para determinar, por medio de fórmulas específicas, cuál ha sido la distancia cubierta por la extensión de una curva.
En otros tiempos, se creía imposible establecer la longitud de un arco (tal como se conoce a las curvas continuas que permiten unir dos puntos determinadas) si éste tenía propiedades irregulares porque, para los matemáticos de la antigüedad, las curvas, a diferencia de las líneas rectas, carecían de una longitud concreta. Por ese entonces, sólo trabajaban con referencias aproximadas que obtenían al sumar todos los lados de un polígono que trazaban en el interior de la curva a evaluar. Siglos más tarde, se modificó la modalidad de cálculo y el proceso comenzó a desarrollarse por medio de técnicas geométricas aplicadas a curvas trascendentes.
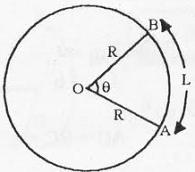
Al examinar una circunferencia, dice la teoría, es posible obtener información de la longitud de su arco a partir de la deducción del radio y la medida del ángulo formado por el par de radios. Conocidos esos datos, se aplica la fórmula L (longitud) = r (radio) * o (ángulo) o bien se calcula la medida del ángulo en radianes.
