Ejemplos de fracciones impropias
Si la información que publicamos tiempo atrás sobre las fracciones y las diversas formas de clasificar a estas estructuras tan empleadas en el ámbito de la Matemática te resultó interesante, este texto también conseguirá atraerte porque gira en torno a las características de las fracciones impropias.
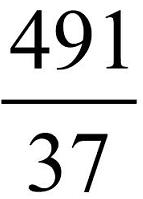 Según la teoría, una fracción se considera impropia cuando se advierte que el numerador es más grande que el denominador. Distinto es el caso de las fracciones propias, en las cuales el numerador es menor que el denominador ya que en la parte inferior de la línea divisoria la cantidad expresada es más grande respecto a la cifra indicada en la parte superior.
Según la teoría, una fracción se considera impropia cuando se advierte que el numerador es más grande que el denominador. Distinto es el caso de las fracciones propias, en las cuales el numerador es menor que el denominador ya que en la parte inferior de la línea divisoria la cantidad expresada es más grande respecto a la cifra indicada en la parte superior.
Ahora que ya hemos recordado el detalle clave que permite identificar a estos dos grupos de fracciones, sólo es cuestión de pensar algunos casos posibles de fracciones impropias. Ustedes pueden proponer infinitas variantes, pero para evitar posibles errores en la interpretación de la teoría, a continuación compartiremos algunos ejemplos concretos de fracciones que cumplen los requisitos para pertenecer al conjunto de las fracciones impropias.
Fracción impropia es, por ejemplo, 18/5 ya que 18 (cifra expresada en el numerador) es superior a 5 (valor del denominador). En base a este modelo específico, entonces, se puede decir que 9/5, 15/3, 17/15, 21/6, 28/18, 37/8, 42/13, 52/17, 56/29, 63/14, 73/12, 74/33, 79/59, 84/21, 87/36, 93/39, 95/90, 98/25, 100/84, 104/82, 120/50, 142/44, 138/27, 256/192, 236/149, 295/74, 283/93, 214/128, 310/150, 319/208, 320/183, 323/181, 339/175 y 345/276 son también parte del infinito grupo de las fracciones impropias.
