Ejemplos de inecuaciones
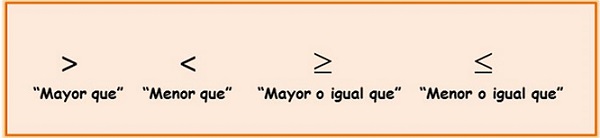
Para poder resolver una inecuación, lo primero que se necesita es tener bien presente y clara la teoría que explica el concepto. La definición más simple y directa permite presentar a las inecuaciones como desigualdades de carácter algebraico donde los miembros están relacionados por los signos correspondientes a “menor que” (<), “menor o igual que” (≤), “mayor que” (>) o “mayor o igual que” (≥).
Para resolverlo se tienen que hallar los valores correspondientes a la variable que brinda la posibilidad de verificarla. Un intervalo o una representación gráfica sirven para expresar la solución de cada inecuación.
Hay, en la práctica, una gran cantidad de inecuaciones, algunas de las cuales detallaremos a continuación para ayudarlos a incorporar datos de interés sobre este tema.
Una de ellas son las inecuaciones equivalentes, que se reconocen cuando se les suma o resta a los dos miembros de una determinada inecuación una misma cifra, cuando a ambas partes se les divide o multiplica por un mismo número, ya sea negativo o positivo.
 A medida que uno domina las inecuaciones es posible hacer operaciones más complejas, resolviendo así inecuaciones de primer grado (presentadas como inecuaciones lineales) o inecuaciones de segundo grado, entre otras.
A medida que uno domina las inecuaciones es posible hacer operaciones más complejas, resolviendo así inecuaciones de primer grado (presentadas como inecuaciones lineales) o inecuaciones de segundo grado, entre otras.
Ahora que repasamos cuestiones teóricas, es posible aplicar los conocimientos para resolver la siguiente inecuación, de la cual figuran todos los pasos necesarios para descubrir el valor de x (la incógnita):
2x – 3 > 55
2x -3 + 3 > 55 + 3
2x > 55 + 3
2x > 58
x > 58/2
x > 29
